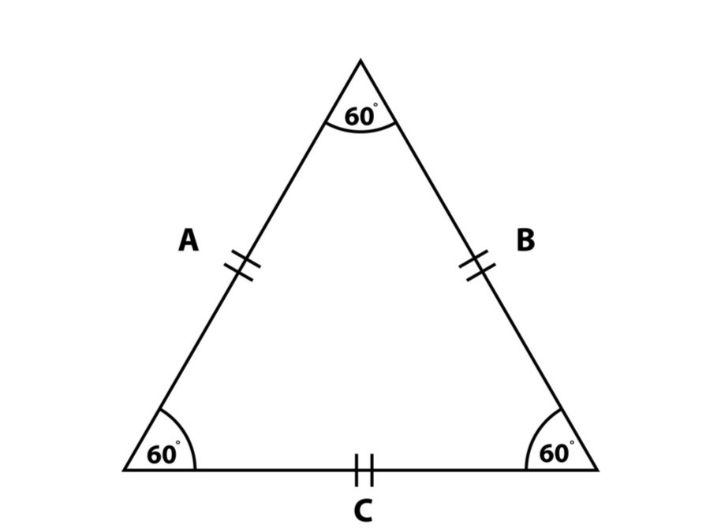
المثلث هو شكل هندسي مغلق أبعاده ثنائية، وفيه 3 زوايا، و3 أضلاع مستقيمة، وعدد أضلاعه يساوي تمامًا عدد زواياه، وتتكون الزوايا فيه من خلال التقاء كل ضلعين، وبالإمكان حساب محيط المثلث بقوانين معينة.
قوانين حساب محيط المثلث
بالإمكان حساب محيط المثلث بقوانين معينة، وهي:
- محيط المثلث: هو مجموع طول كل ضلع من أضلاع المثلث، أي إذا كانت أطوال أضلاعه هي أ، ب، ج، فمحيطه = أ + ب + ج.
- محيط المثلث متساوي الأضلاع: يمكن حساب محيط المثلث متساوي الأضلاع إذا كان طول ضلع فيه هو أ بالقانون التالي: أ3x.
- محيط المثلث متساوي الساقين: يُحسب محيط المثلث متساوي الساقين الذي طول ضلع من الضلعين المتساويين فيه هو أ، وطول الضلع الثالث هو ب من خلال القانون التالي: 2أ + ب.
- محيط المثلث القائم: محيط المثلث القائم الذي الأضلاع فيه هي أ ، ب، والوتر، بالقانون التالي أ + ب + الوتر، ويُحسب محيط المثلث الذي يكون فيه طول الوتر مجهولًا بحساب طول الوتر أولًا بواسطة نظرية فيثاغورس، فيُصبح قانون محيط المثلث القائم أ + ب + (أ2 + ب2)√
أمثلة على كيفية حساب محيط المثلث
فيما يلي أمثلة على كيفية حساب محيط المثلث:
- ما محيط مثلث أطوال أضلاعه هي: 5 سم، 2 سم، 4 سم؟
محيط المثلث = أ + ب + ج
= 5 + 2 + 4 = 11 سم.
- ما طول الضلع المجهول لمثلث محيطه 40 سم، وطول ضلعيه الآخرين 10 سم؟
هذا المثلث مثلثاً متساوي الساقين
محيط المثلث متساوي الساقين= أ + 2×ب
40 = أ + 2×10
40 = أ + 20
40 – 20 = أ
20 سم = أ
- ما محيط مثلث متساوي الأضلاع طول ضلعه 15 سم؟
محيط المثلث متساوي الأضلاع = أ×3
= 15 × 3
= 45 سم
ما محيط مثلث أطوال أضلاعه: 4 م، 8 م، 12 م.
محيط المثلث = أ + ب + ج
= 4 + 8 + 12
= 24 م.
- ما محيط مثلث متساوي الساقين طول أحد أضلاعه 5.5 سم، وطول الضلعين المتساويين فيه 6 سم؟
محيط المثلث متساوي الساقين = أ + 2 ب
= 5.5 + (2 × 6)
= 17.5 سم